Combination of Resistors - Series and Parallel
Combination of Resistors - Series and Parallel: Overview
This topic covers concepts, such as, Parallel Combination of Resistors, Series Combination of Resistors, Infinite Ladder Problems of Resistors & Combination of Resistors etc.
Important Questions on Combination of Resistors - Series and Parallel
A wire of resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 4.0 volt battery. The current drawn from the battery is:
A (i) series (ii) parallel combination of two given resistors is connected, one – by – one, across a cell. In which will the terminal potential difference, across the cell, have a higher value?
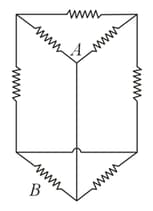
(i) Calculate the equivalent resistance of the given electrical network between points and .
(ii) Also calculate the current through , if a source is connected between and , and the value of is assumed as .
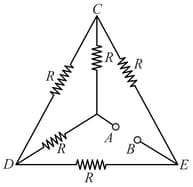
You are given resistors, each of resistance . These are first connected to get the minimum possible resistance. In the second case, these are again connected differently to get maximum possible resistance. The ratio between the minimum and maximum values of resistance so obtained is
You are given ‘n’ resistors, each of resistance ‘r’. These are first connected to get minimum possible resistance. In the second case, these are again connected differently to get maximum possible resistance. The ratio between the minimum and maximum values of resistance so obtained is
Draw the unit step for the infinite ladder drawn below. What is the application of finding this step in solving network-related problems?
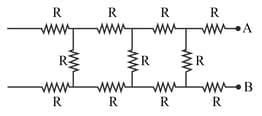
An infinite network consists of repeated units. The equivalent resistance of this network of resistors does not change if:
Find the equivalent resistance of the following infinite network:
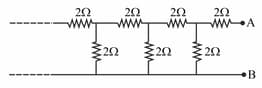
Find the current drawn from a supply by the infinite network shown in the figure below.
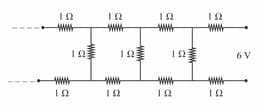
Two infinite ladders of resistors are connected through a resistor CD as shown below. The equivalent resistance between points A and B is:
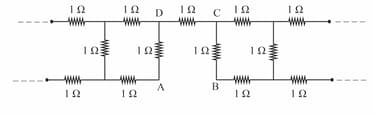
Four infinite ladder alike networks are combined as shown in figure .Each resistance is . The equivalent resistance between and is and between and is Let ratio then find the value of .
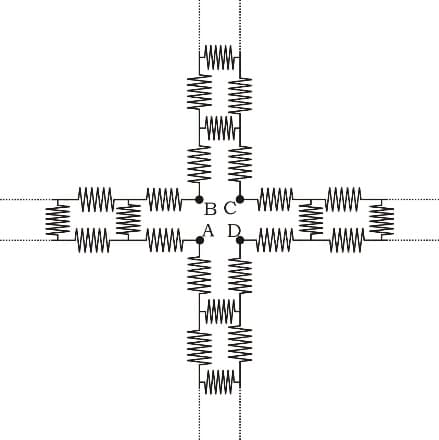
A wire has a resistance of is bent in the following shape. The effective resistance between and is . The value of is
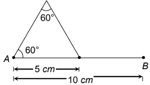
Two wires of the same dimension but resistivity , and are connected in series. The equivalent resistivity of the combination is
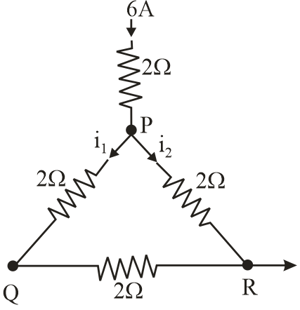
A current of 6 A enters one corner of an equilateral triangle having wires of resistance each and leaves by the corner The currents in ampere is _______.
Three resistors are joined to form a triangle . The resistance of the sides and are and respectively. Find the equivalent resistance between points and .
The equivalent resistance of the parallel combination of two resistors of and is _____.
Three resistors , and are joined in parallel and connected to battery of 20V and negligible resistance. Find the equivalent resistance.
Effective resistance between points and for the following network is: (each branch of resistance is and there is one connecting wire)
Two resistances and are connected in parallel. The equivalent resistance is
The smallest resistance that can be obtained by the combination of resistors, each of resistance is,
